Wzory skróconego mnożenia stopnia 2

Wzory skróconego mnożenia usprawniają wykonywanie obliczeń algebraicznych. Pozwalają m.in. na rozkładanie wyrażeń algebraicznych na czynniki oraz usuwanie niewymierności z mianownika ułamka. Poniżej zostały zebrane wzory skróconego mnożenia stopnia drugiego obowiązujące na poziomie podstawowym.

Kwadrat sumy dwóch wyrażeń

(a + b)² = a² + 2ab + b²

Zapis słowny: Kwadrat sumy dwóch wyrażeń jest równy sumie kwadratów pierwszego i drugiego wyrażenia powiększonej o podwojony iloczyn obu wyrażeń. 

Geometryczne uzasadnienie wzoru:

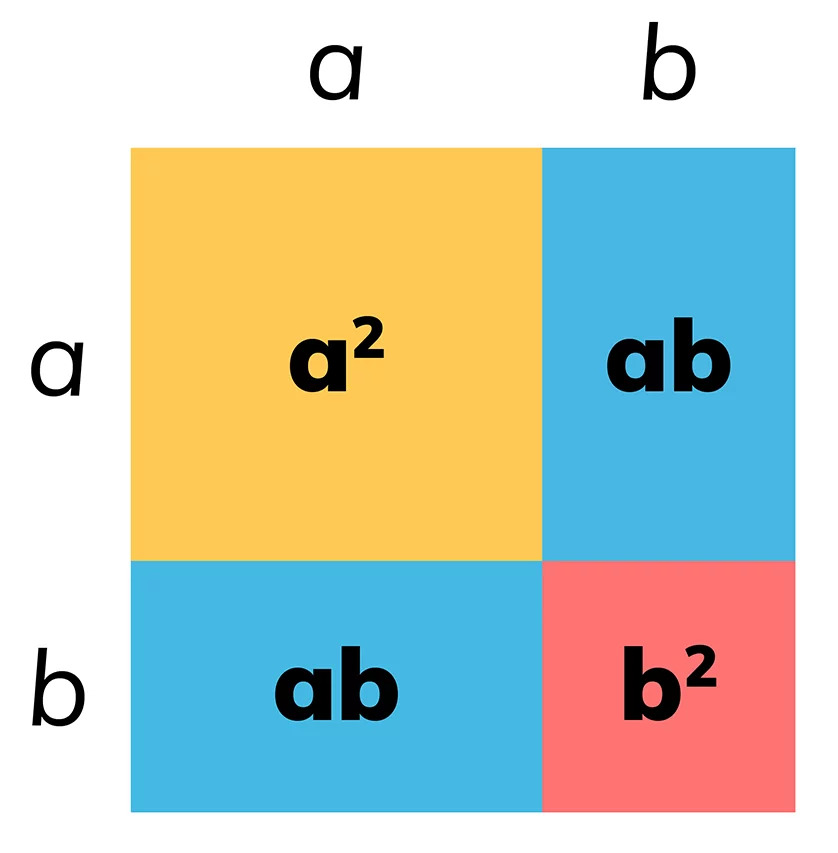
Kwadrat o boku długości (a + b) możemy podzielić na dwa mniejsze kwadraty o polach a² i b² oraz dwa prostokąty o polu ab.

Pole kwadratu jest równe sumie pól czterech otrzymanych części, czyli: (a + b)² = a² + 2ab + b².

Przykład

Używając wzoru skróconego mnożenia na kwadrat sumy, zapiszemy wyrażenie (x + 4)² w postaci sumy algebraicznej:

(x + 4)² = x² + 2 · x · 4 + 4²

Przykład

Używając wzoru skróconego mnożenia na kwadrat sumy, zapiszemy wyrażenie (√6 + 3)² w postaci sumy algebraicznej:

(√6 + 3)² = (√6)² + 2 · √6 · 3 + 3² = 6 + 6√6 + 9 = 15 + 6√6

Uwaga

Kiedy stosujemy wzór skróconego mnożenia na kwadrat sumy dwóch wyrażeń, to pamiętajmy, że nie muszą być one wyrażeniami dodatnimi.

Np. jeśli chcemy obliczyć wartość wyrażenia (y – 3)², korzystając ze wzoru na kwadrat sumy, to zauważymy, że podnosząc do kwadratu różnicę (y – 3) możemy zapisać w postaci sumy (y + (-3)) i wtedy otrzymujemy:

(y – 3)² = (y + (-3))² = y² + 2 · y · (-3) + (-3)² = y² – 6y + 9

Uwaga

Powyższy wzór możemy również stosować w przypadku, gdy chcemy zapisać w postaci sumy algebraicznej wyrażenie (√3 + √5 + 4)²; wystarczy, że zapiszemy je np. w postaci ((√3 + √5 )+ 4)². Wtedy otrzymujemy:

(√3 + √5 + 4)² = ((√3 + √5)+ 4)² = (√3 + √5)² + 2 · (√3 + √5) · 4 + 4²

Kwadrat różnicy dwóch wyrażeń

(a – b)² = a² – 2ab + b²

Zapis słowny: Kwadrat różnicy dwóch wyrażeń jest równy sumie kwadratów pierwszego i drugiego wyrażenia pomniejszonej o podwojony iloczyn obu wyrażeń. 

Geometryczne uzasadnienie wzoru:

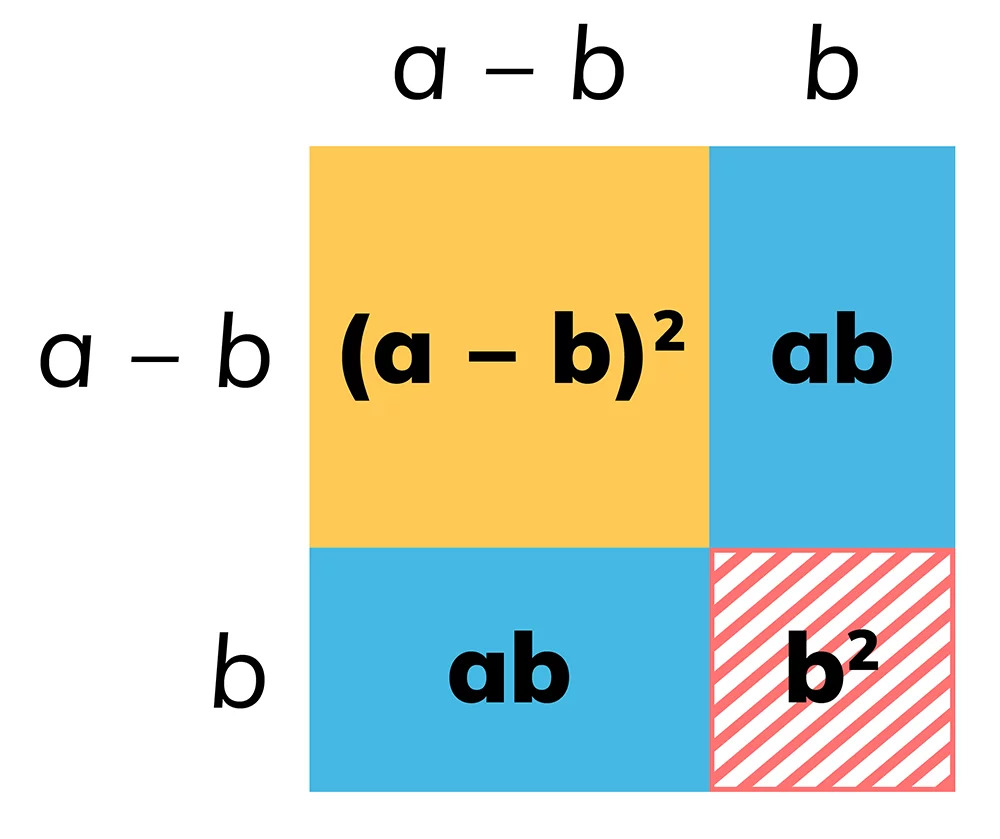
Kwadrat o boku długości a dzielimy tak jak na powyższym rysunku (a > b).
Pole kwadratu jest równe P = a².

Zauważmy, że pole rozważanego czworokąta możemy także policzyć w następujący sposób: do pola kwadratu o boku długości (a – b) dodajemy pola dwóch prostokątów o wymiarach a x b i odejmujemy pole kwadratu o boku długości b (gdyż pole tego kwadratu policzyliśmy dwa razy).
P = (a – b)² + 2ab – b²

Z obu równości otrzymujemy:
a² = (a – b)² + 2ab – b²
a² -2ab + b² = (a – b)²

Przykład

Używając wzoru skróconego mnożenia na kwadrat różnicy, zapiszemy wyrażenie (2x – 5)² w postaci sumy algebraicznej:

(2x – 5)² = (2x)² – 2 · 2x · 5 + 5² = 4x² – 20x + 25

Przykład

Używając wzoru skróconego mnożenia na kwadrat różnicy, zapiszemy wyrażenie (3√8 – 7√2)² w postaci sumy algebraicznej:

(3√8 – 7√2)² = (3√8)² – 2 · 3√8 · 7√2 + (7√2)² = 9 · 8 – 42√16 + 49 · 2 = 72 – 42 · 4 + 98 = 170 – 168 = 2

Różnica kwadratów dwóch wyrażeń

a² – b² = (a + b)(a – b)

Zapis słowny: Różnica kwadratów dwóch wyrażeń jest równa iloczynowi sumy i różnicy tych wyrażeń. 

Geometryczne uzasadnienie wzoru:

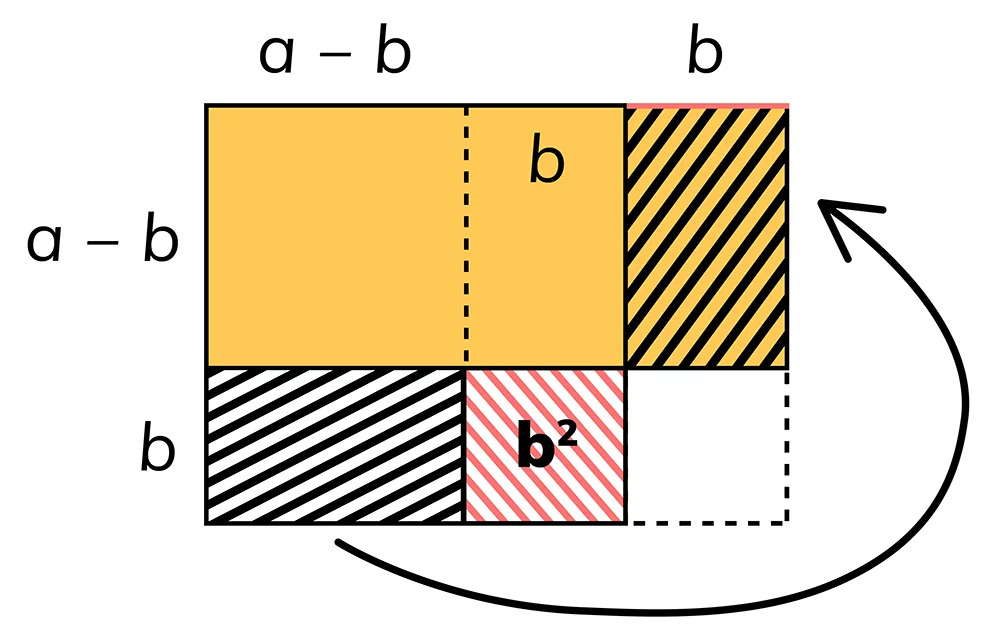
Pole prostokąta o bokach długości (a + b) i (a – b) (żółty prostokąt) jest równe polu kwadratu o boku długości a pomniejszonemu o pole kwadratu o boku długości b, czyli: (a + b)(a – b) = a² – b².

Przykład

Używając wzoru skróconego mnożenia na różnicę kwadratów, zapiszemy wyrażenie (3 – 2x)(3 + 2x) w postaci sumy algebraicznej:

(3 – 2x)(3 + 2x) = 3² – (2x)² = 9 – 4x²

Przykład

Używając wzoru skróconego mnożenia na różnicę kwadratów, zapiszemy wyrażenie (2a√8 + 3)(2a√8 – 3) w postaci sumy algebraicznej:

(2a√8 + 3)(2a√8 – 3) = (2a√8)² – 3² = 4a² · 8 – 9 = 32a² – 9

Do tej pory rozważaliśmy przykłady, w których przekształcaliśmy iloczyny na sumy algebraiczne. Jednak wzorów skróconego mnożenia możemy używać, wykonując operację odwrotną, czyli gdy chcemy zapisać podaną sumę algebraiczną w postaci iloczynu.

Prześledźmy to na przykładach.

Przykład

Rozłożymy wyrażenie 4 + 4m + m² na czynniki.
Zauważmy, że w podanym wyrażeniu mamy sumę kwadratów 2 i m powiększoną o podwojony iloczyn liczb 2 i m, czyli korzystając ze wzoru skróconego mnożenia na kwadrat sumy, otrzymujemy:

4 + 4m + m² = 2² + 2 · 2 · m + m² = (2 + m)²

Przykład

Rozłożymy wyrażenie 25x² + 1 + 10x na czynniki.
Zauważmy, że 25x² = (5x)², więc w podanym wyrażeniu mamy sumę kwadratów (5x)² i 1² powiększoną o podwojony iloczyn liczb 5x i 1, czyli korzystając ze wzoru skróconego mnożenia na kwadrat różnicy, mamy:

25x² + 1 + 10x = (5x)² + 2 · 5x · 1 + 1² = (5x + 1)²

Przykład

Rozłożymy wyrażenie 36y² – 81 na czynniki.
Zauważmy, że 36y² = (6y)² oraz 9² = 81 więc podane wyrażenie jest różnicą kwadratów (6y)² i 9², czyli korzystając ze wzoru skróconego mnożenia na różnicę kwadratów dostajemy:

36y² – 81 = (6y)² – 9² = (6y – 9)(6y + 9)

Usuwanie niewymierności z mianownika

Korzystając ze wzorów skróconego mnożenia, możemy także usuwać niewymierności z mianownika ułamka, co ilustruje poniższy przykład.

Przykład

Usuniemy niewymierność z mianownika ułamka:

\dfrac{5}{\sqrt{7} + 1}

W mianowniku powyższego ułamka mamy sumę liczb √7 i 1.
Zauważmy, że jeśli pomnożymy ją przez różnicę tych samych liczb, czyli przez √7 – 1, to zgodnie ze wzorem skróconego mnożenia na różnicę kwadratów, otrzymamy:

(√7 + 1)(√7 – 1) = √7² – 1² = 7 – 1 = 6

Otrzymana liczba jest wymierna, co oznacza, że jeśli licznik i mianownik podanego ułamka pomnożymy przez (√7 – 1), to usuniemy z jego mianownika niewymierność. Dostajemy:

\dfrac{5 \cdot (\sqrt{7} - 1)}{(\sqrt{7} + 1) \cdot (\sqrt{7} - 1)} = \dfrac{5\sqrt{7} - 5}{\sqrt{7^2} - 1^2} = \dfrac{5\sqrt{7} - 5}{7 - 1} =  \dfrac{5\sqrt{7} - 5}{6}