Kilka słów o pracy i energii mechanicznej

W życiu codziennym praktycznie każdego dnia mówi się o wykonywaniu pracy, czy to zarobkowej, czy w domu. Podobnie jest z energią. Często mówimy, że mamy bardzo dużo energii, aby zabrać się do pracy. Zastanówmy się nad tymi pojęciami w kontekście fizyki.

Praca mechaniczna

Znaczna część naszego życia kręci się wokół pracy. Niezależnie od tego, czy jest to praca zawodowa, czy wykonywana w ramach zadań szkolnych, przeważnie stawia przed nami wyzwania, którym staramy się podołać. Jednak termin „praca” jest również bardzo mocno związany z fizyką. To jedno z najważniejszych pojęć (zaraz obok siły), którego rozważania prowadzą do poznania podstaw zasad działania i budowy wszechświata. Na lekcjach fizyki będziemy się uczyć o pracy mechanicznej, termodynamicznej, objętościowej oraz prądu elektrycznego. Teraz skupmy się na tym pierwszym rodzaju pracy, a mianowicie na pracy mechanicznej, czyli ściśle związanej z ruchem ciała oraz siłami działającymi na to ciało.

Mówimy, że praca mechaniczna jest wykonywana, gdy na ciało działa siła, w wyniku czego ciało to ulega przemieszczeniu lub odkształceniu. Pracę w fizyce oznaczamy literą W od angielskiego słowa work, czyli po prostu „praca”.

Praca mechaniczna jest wykonywana, gdy na ciało działa siła, a ono porusza się w kierunku innym niż kierunek prostopadły do kierunku działania siły. Pracę mechaniczną możemy obliczyć za pomocą wzoru:

W=F \cdot s

gdzie F jest wartością siły działającej na ciało, które w czasie ruchu przebywa drogę równą s, a kierunek wektora siły jest równoległy do kierunku wektora przemieszczenia.

Istotne jest tutaj również pojęcie kierunku ruchu oraz związane z nim przemieszczenie, czyli wektor łączący położenie początkowe i końcowe ciała. W zależności od tego czy siła działa zgodnie z kierunkiem ruchu ciała, czy przeciwnie do niego, możemy przyjąć, że wówczas praca wykonana przez tą siłę wynosi:

W=-F \cdot s

Taki przypadek mamy, gdy pracę wykonują na przykład siły tarcia kinetycznego. Praca jest wielkością skalarną i nie może być ujemna. Znak minus jest umowny – informuje nas, że w tym przypadku zwroty wektora siły oraz przemieszczenia są przeciwne.

Jak wspomniano powyżej, kierunek działania siły nie może być prostopadły do kierunku wektora przemieszczenia. Wydaje się to być całkiem naturalne, ponieważ wówczas nie ma siły, która powodowałaby przesunięcie tego ciała. W takim przypadku praca mechaniczna nie jest wykonywana i piszemy, że ma zerową wartość:

W=0

Możemy powyższe przypadki ująć na następującym schemacie.

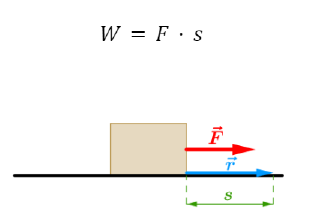
Ryc. 1.1. Na klocek działa siła zwrócona zgodnie z kierunkiem ruchu

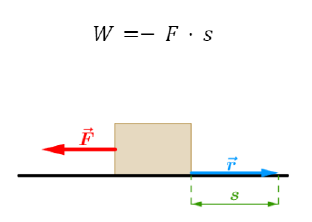
Ryc. 1.2. Na klocek działa siła hamująca, zwrócona przeciwnie do kierunku ruchu

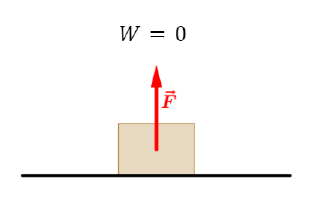
Ryc. 1.3. Na klocek działa siła prostopadła do kierunku ruchu

Zauważmy, że gdy praca mechaniczna jest wykonywana, to w każdym przypadku możemy wyrazić ją jako iloczyn wartości siły i przemieszczenia. Oznacza to, że jednostkę wykonanej pracy możemy określić przez jednostkę siły i drogi:

[W]=[F]\cdot[s]=1N\cdot 1m

Jednostką pracy mechanicznej jest dżul, który oznaczamy literą J. Nazwa ta pochodzi od nazwiska brytyjskiego fizyka Jamesa Prescotta Joule’a, który prowadził badania związane z przemianami energii mechanicznej. Możemy zapisać, że dżul wyrażony przy pomocy podstawowych jednostek SI ma postać:

1 J = 1 N \cdot m = 1 kg \cdot \frac{m}{s^2} \cdot m = 1 kg \cdot \frac{m^2}{s^2} 

Energia mechaniczna – rodzaje

Rozmawiając z innymi, często używamy zwrotów: „Ale mam dzisiaj dużo energii!”, „Rozpiera mnie energia”, czy „Wyczerpałem wszystkie pokłady energii”. Okazuje się, że świetnie opisują one energię jako pojęcie fizyczne.

Zastanówmy się, czym jest energia w znaczeniu badawczym!

Zgodnie z definicją, energia jest to wielkość fizyczna, która charakteryzuje stan układu. Oznaczamy ją literą E od angielskiego słowa energy, czyli „energia”. Często również określa się tym pojęciem siły witalne organizmu, co jest również związane z energią fizyczną, gdyż ich pochodzenie wynika z pewnych przemian energii. Rozróżniamy wiele form energii, takich jak na przykład energia chemiczna, jądrowa, elektryczna czy magnetyczna. Teraz jednak skupimy się na jej szczególnym rodzaju, a mianowicie na energii mechanicznej.

Praca wykonana w układzie zamienia energię mechaniczną układu. Oznacza to, że jeżeli w układzie fizycznym została wykonana pewna praca, to zmienił się stan tego układu, a zatem i jego energia:

\Delta E=W

gdzie:

\Delta E- zmiana energii

W- praca wykonana w układzie.

W powyższej zależności grecka duża litera Δ (delta) mówi nam o tym, że mamy do czynienia ze zmianą, czyli różnicą pomiędzy stanem końcowym a początkowym układu:

\Delta E=E{_{końcowa}}-E{_{początkowa}}

Skoro jednostką pracy jest dżul, to jednostką zmiany energii również jest dżul. Ponieważ zmiana energii odpowiada różnicy pomiędzy energią końcową a początkową, to każda z tych energii musi być również wyrażona za pomocą dżuli. Oznacza to, że energię, podobnie jak pracę, będzie wyrażać za pomocą dżuli.

Rozróżniamy dwa rodzaje energii mechanicznej: energię potencjalną, wynikającą z położenia lub odkształcenia ciała oraz energię kinetyczną, związaną z ruchem ciała.

Energia potencjalna ciężkości

Na każde ciało na Ziemi działa siła ciężkości. Dla niezbyt dużych wysokości nad powierzchnią Ziemi przyspieszenie grawitacyjne nie zmienia się. Oznacza to, że jeżeli chcemy podnieść pewne ciało na dowolną wysokość h, to musimy wykonać pracę, która będzie przeciwdziałać sile ciężkości tego ciała. Zauważmy, że siła, z jaką musimy działać na to ciało, powinna równoważyć ciężar tego ciała, czyli będzie miała ona przeciwny zwrot do siły ciężkości, ale taką samą wartość jak ta siła. Wówczas wykonamy pracę równą:

W=F_c\cdot h

gdzie:

W- praca wykonana przez nas,

F_c=m\cdot g- wartość ciężaru ciała, gdzie m jest masą, g jest wartością przyspieszenia ziemskiego,

h- wysokość, na jaką wzniosło się ciało (droga przebyta przez ciało w czasie podnoszenia).

Zmiana położenia ciała względem pewnego położenia początkowego powoduje zmianę energii potencjalnej tego ciała. Ponadto zmiana energii potencjalnej ciała jest równa pracy wykonanej przez nas:

\Delta E_p=W

Energię potencjalną wyznaczamy zawsze względem pewnego położenia zerowego (np. powierzchni Ziemi). Jeżeli w naszym przypadku początkowo ciało było na Ziemi, to przyjmujemy, że jest to nasz poziom zerowy i w tym punkcie początkowa energia potencjalna zawsze przyjmie zerową wartość:

E{_{p.początkowa}}=0

Potencjalna energia końcowa po wzniesieniu się ciała na podaną wysokość będzie odpowiadała energii potencjalnej tego ciała dokładnie w tym punkcie:

E{_{p.końcowa}}=E_p

Oznacza to, że w ogólnym przypadku energię potencjalną ciała E_p​ na dowolnej wysokości h możemy obliczać za pomocą wzoru wynikającego z następującego wyprowadzenia:

\Delta E_p=W

E{_{p.końcowa}}-E{_{p.początkowa}}=W

E {_ {p}} - 0 = F{_ {c}} \cdot h

E {_{p}} = m \cdot g \cdot h

W ten sposób otrzymaliśmy energię potencjalną ciężkości (grawitacji) ciała na dowolnej wysokości nad powierzchnią Ziemi. Zauważmy, że zależy ona od masy ciała oraz wysokości, na jakiej znajduje się to ciało.

Energia potencjalna sprężystości

Zmiana energii potencjalnej w przestrzeni może być związana nie tylko ze zmianą położenia ciała, ale również z odkształceniem ciała. Najlepszym tego przykładem jest zmiana energii potencjalnej ciała zawieszonego na sprężynie. Siła odkształcająca sprężynę to siła sprężystości, której wartość przedstawimy wzorem:

F_s=k\cdot x

gdzie:

k- współczynnik sprężystości (zależy od właściwości materiału odkształacającego się ciała),

 x- długość, o jaką wydłużyła się sprężyna.

Zastanówmy się, jak będzie zmieniała się energia potencjalna odkształconego ciała, czyli energia potencjalna sprężystości.

Zauważmy, że im większe będzie odkształcenie ciała, czyli na przykład im bardziej wydłużymy sprężynę, tym większa siła będzie na nią działała. Siła sprężystości jest wprost proporcjonalna do wydłużenia sprężyny, co możemy przedstawić na wykresie:

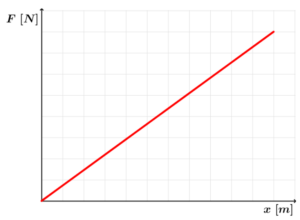
Ryc. 2. Wykres zależności wartości siły sprężystości od wydłużenia

Mamy ogólną prawidłowość, która mówi nam, że pole pod wykresem zależności siły działającej na ciało od zmiany położenia tego ciała lub odkształcenia odpowiada pracy wykonanej nad tym ciałem. Z wykresu wynika, że dla dowolnego wydłużenia x praca wykonana przez siłę sprężystości będzie odpowiadała polu trójkąta pod tym wykresem:

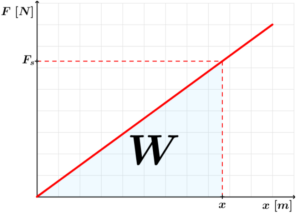
Ryc. 3. Wykres zależności wartości siły sprężystości od wydłużenia z oznaczoną pracą wykonaną przez siłę sprężystości przy odkształceniu ciała o x

Zauważmy, że mamy do czynienia z trójkątem prostokątnym, którego długości boków odpowiadają wielkościom F_s​ i x. Oznacza to, że praca wykonana przez siłę sprężystości wynosi:

W = \frac{1}{2} \cdot F {\scriptscriptstyle{s}} \cdot x

Zmiana energii potencjalnej sprężystości będzie odpowiadała pracy wykonanej przy zmianie odkształcenia ciała:

\Delta E{_{p.s.}}=W

Gdy ciało nie jest odkształcone, przyjmujemy, że nie posiada energii potencjalnej sprężystości, czyli podobnie jak w przypadku energii potencjalnej ciężkości, początkowa energia potencjalna sprężystości jest zerowa:

E{_{p.s.początkowa}}=0

Potencjalna energia końcowa po odkształceniu będzie odpowiadała energii potencjalnej sprężystości tego ciała dokładnie przy tym wydłużeniu E_{p.s.}​:

E{_{p.s.końcowa}}=E{_{p.s.}}

Oznacza to, że w ogólnym przypadku energię potencjalną sprężystości dla dowolnego wydłużenia (odkształcenia) x możemy opisać za pomocą wzoru:

\Delta E {_{p.s.}} = W

E {_{p.s. końcowa}} - E {_{p.s. początkowa}} = W

E {_{p.s.}} - 0 = \dfrac{1}{2} \cdot F_s \cdot x

E {_{p.s.}} = \frac {1}{2} \cdot k \cdot x \cdot x

E {_{p.s.}} = \frac {1}{2} \cdot k \cdot x^2

Z powyższego wyprowadzenia otrzymaliśmy energię potencjalną sprężystości układu przy dowolnym jego odkształceniu (np. wydłużenie sprężyny).

Energia kinetyczna

Energia kinetyczna jest energią związaną z ruchem ciała. Skoro ciało się porusza, to posiada pewną prędkość, którą nada mu działająca na nie siła. Wykona ona wówczas pracę. W tym przypadku mało istotną kwestią jest dla nas pochodzenie tej siły, dlatego będzie to siła wypadkowej, której wartość zgodnie z II zasadą dynamiki Newtona przedstawimy wzorem:

F=m\cdot a

gdzie:

m- masa poruszającego się ciała,

a- wartość przyspieszenia, z jakim porusza się to ciało.

Skoro na ciało działa siła, to porusza się ono z przyspieszeniem. Wówczas droga, jaką przebywa to ciało w tym ruchu, może zostać obliczona za pomocą wzoru:

s = v _0 t + \frac{1}{2}at^2

gdzie:

v_0- szybkość początkowa, jaką ciało posiadało w chwili, gdy zaczynała działać na nie siła,

t- czas, w jakim poruszało się ciało, czyli czas działania na nie siły,

a- wartość przyspieszenia ciała.

Zgodnie z definicją przyspieszenia jego wartość możemy przedstawić wzorem:

a = \frac{\Delta{v}}{\Delta{t}} 

gdzie:

\Delta v=v-v_0- miana szybkości ciała w czasie ruchu, przy czym v jest szybkością końcową tego ciała, a v_0 jest szybkością początkową ciała,

\Delta t=t- zmiana czasu, w jakim następuje zmiana szybkości, która odpowiada czasowi, w jakim siła działa na ciało.

Oznacza to, że praca wykonana podczas nadawania ciału pewnej szybkości v ma postać:

W=F\cdot s

Podstawiamy wyrażenia na wartość siły i drogi:

W = m \cdot a\cdot(v_0t + \frac{1}{2}at^2)

Podstawiamy zależność opisującą przyspieszenie:

W = m\cdot\frac{\Delta{v}}{\Delta{t}}\cdot(v_0t + \frac{1}{2}\cdot\frac{\Delta{v}}{\Delta{t}}\cdot t^2)

W = m\cdot\frac{{v - v _0}}{t}\cdot(v_0t + \frac{1}{2}\cdot\frac{{v - v _0}}{t}\cdot t^2)

W = m\cdot\frac{{v - v _0}}{t}\cdot(v_0t + \frac{1}{2}\cdot{(v - v _0})\cdot t)

W = m\cdot\frac{{v - v _0}}{t}\cdot(v_0t + \frac{1}{2}vt-\frac{1}{2}{v _0t})

W = m\cdot\frac{{v - v _0}}{t}\cdot(\frac{1}{2}vt + \frac{1}{2}{v _0t})

W = m\cdot\frac{{v - v _0}}{t}\cdot\frac{1}{2}t \cdot(v+v_0)

W =\frac{1}{2}m \cdot(v-v_0)\cdot(v+v_0)

Wymnażamy przez siebie jednomiany w nawiasach:

W = \frac{1}{2}m\cdot[v\cdot v+v_0\cdot v -v_0\cdot v-v_0\cdot v_0]

Skracamy wyrażenia podobne:

W = \frac{1}{2}m\cdot[ v^2-{v_{0}}^2]

Zmiana energii kinetycznej będzie odpowiadała pracy wykonanej przy zmianie szybkości ciała:

\Delta{E}_k=W

Załóżmy, że na początku ciało się nie porusza, czyli wartość jego prędkości początkowej jest zerowa:

v_0=0

Skoro ciało się nie porusza, to jego początkowa energia kinetyczna będzie również zerowa:

E{_{k.początkowa}}=0

Oznacza to, że praca, jaka została wykonana przy nadawaniu ciału szybkości v, ma postać:

W=\frac{1}{2}m\cdot[v^2-0^2]

W=\frac{1}{2}mv^2

Wówczas energia końcowa dla dowolnej szybkości v uzyskanej przez to ciało odpowiada energii kinetycznej ciała dokładnie dla tej szybkości:

E{_{k.końcowa}}=E_k

Zatem:

\Delta E_k=W

E{_{k. końcowa}}-E{_{k. początkowa}}=W

E{_{k}}-0=\frac{1}{2}mv^2

E{_{k}}=\frac{1}{2}mv^2

Z powyższego wyprowadzenia otrzymaliśmy energię kinetyczną układu dla dowolnej szybkości, z jaką ten układ się porusza.

Zasada zachowania energii – przykłady zastosowania

Energia występuje w różnych postaciach i nie może być niszczona ani samoistnie wytworzona. Jest przekazywana w rozmaitych procesach fizycznych, skąd wynika zasada zachowania energii. Możemy ją sformułować w następujący sposób:

W izolowanym układzie suma wszystkich rodzajów energii układu jest stała w czasie.

Oznacza to, że pomimo upływu czasu suma energii potencjalnej i kinetycznej ciała jest taka sama w każdym punkcie rozważanego układu. Możemy ogólnie przedstawić ją wzorem:

E_c=E_k+E_p

Zobaczmy, jak stosować tę zasadę w praktyce na najbardziej popularnych przykładach.

Spadek swobodny ciała

Ze spadkiem swobodnym ciała mamy do czynienia, gdy pominiemy wpływ siły oporów ruchu oraz tarcia w czasie ruchu tego ciała. Zakładamy, że ciało znajduje się na pewnej wysokości, z której spada swobodnie. Skoro ciało fizyczne (np. piłka) spada swobodnie, to oznacza, że na początku ruchu nie nadano jej żadnej szybkości początkowej i porusza się ono w wyniku działania na nie siły ciężkości. Załóżmy, że wysokość z jakiej spada to ciało wynosi H. Zastanówmy się nad przemianami energii tego ciała na kilku wybranych punktach pośrednich w tym spadku (np. w \frac{3}{4} maksymalnej wysokości, połowie wysokości i \frac{1}{4} całkowitej wysokości) oraz na maksymalnej wysokości oraz na podłożu. Możemy ten przypadek przedstawić następującym schematem:

Ryc. 4. Przedstawienie energii potencjalnej ciężkości i kinetycznej w układzie, w którym mamy do czynienia ze spadkiem swobodnym

W powyższym przykładzie poszczególne wysokości wynoszą:

h_0=0

h_1=\frac{1}{4}H

h_2=\frac{1}{2}H

h_3=\frac{3}{4}H

h_4=H

Wówczas tak naprawdę energie potencjalne tego ciała na tych wysokościach możemy przedstawić jako:

E{_{p.0}}=mg\cdot0=0

E{_{p.1}}=mg\cdot\frac{1}{4}H=\frac{1}{4}mgH

E{_{p.2}}=mg\cdot\frac{1}{2}H=\frac{1}{2}mgH

E{_{p.3}}=mg\cdot\frac{3}{4}H=\frac{3}{4}mgH

E{_{p.4}}=mgH

Zgodnie z zasadą zachowania energii całkowita energia mechaniczna układu w każdym punkcie spadku tego ciała jest taka sama, czyli prawdziwe jest równanie:

E{_{p.0}}+E{_{k.0}}=E{_{p.1}}+E{_{k.1}}=E{_{p.2}}+E{_{k.2}}=

=E{_{p.3}}+E{_{k.3}}=E{_{p.4}}+E{_{k.4}}

Łatwo możemy wyznaczyć wartości szybkości tego ciała na każdej z tych wysokości, korzystając z zasady zachowania energii.

1.\ {\text{dla }} h_4=H:

v_4=0, {\text{czyli }}E{_{k.4}}=0

2.\ {\text{dla }} h_3=\frac{3}{4}H:

E{_{p.3}}+E{_{k.3}}=E{_{p.4}}+E{_{k.4}}

\frac{3}{4}mgH + \frac{1}{2}mv{_3}^2=mgH+0

v{_3}^2=\frac{1}{2}gH

v{_3}=\sqrt{\frac{1}{2}gH}

3.\ {\text{dla }} h_2=\frac{1}{2}H:

E{_{p.2}}+E{_{k.2}}=E{_{p.4}}+E{_{k.4}}

\frac{1}{2}mgH + \frac{1}{2}mv{_2}^2=mgH+0

v{_2}^2=gH

v{_2}=\sqrt{gH}

4.\ {\text{dla }} h_1=\frac{1}{2}H:

E{_{p.1}}+E{_{k.1}}=E{_{p.4}}+E{_{k.4}}

\frac{1}{4}mgH + \frac{1}{2}mv{_1}^2=mgH+0

v{_1}^2=\frac{3}{2}gH

v{_2}=\sqrt{\frac{3}{2}gH}

5.\ {\text{dla }} h_0=0:

E{_{p.0}}+E{_{k.0}}=E{_{p.4}}+E{_{k.4}}

0+ \frac{1}{2}mv{_0}^2=mgH+0

v{_0}^2=2gH

v{_0}=\sqrt{2gH}

Zauważmy, że żadna z wyznaczonych szybkości nie zależy od masy ciała, a jedynie od wysokości, z której spada to ciało. Kolejnym ważnym wnioskiem jest fakt, że szybkość ciała wzrasta w czasie spadku. Jest to zgodne z naszą wiedzą z kinematyki. Jeżeli zastosujemy definicję przyspieszenia i wzór na drogę w ruchu jednostajnie przyspieszonym, to powinniśmy otrzymać dokładnie takie same wyniki!

Wahadło matematyczne

Wahadło matematyczne w czasie ruchu drgającego wznosi się na pewną maksymalną wysokość, odchylając się w tym samym czasie na maksymalną odległość odpowiadającą amplitudzie drgań.

Przeanalizujmy przemiany energii takiego wahadła, gdy wychylimy je z położenia równowagi do amplitudy.

• Dla x = -A mamy wahadło matematyczne, którego wysokość nad najniższym możliwym położeniem jest największa. W tym punkcie wahadło zatrzymuje się, a jego szybkość jest zerowa. Oznacza to, że energia potencjalna jest wtedy największa, a energia kinetyczna przyjmuje zerową wartość.
• Dla x = 0 mamy położenie równowagi tego wahadła. Wówczas wahadło znajduje się najniżej, a jego energia potencjalna ciężkości przyjmuje zerową wartość. Zatem zgodnie z zasadą zachowania energii, energia kinetyczna wahadła w tym punkcie będzie największa, co oznacza że w położeniu równowagi prędkość liniowa tego wahadła przyjmie największą możliwą wartość.
• Dla x = A mamy wahadło matematyczne odchylone maksymalnie od położenia równowagi w przeciwną stronę niż w chwili początkowej ruchu. Jednak tak samo jak w przypadku x = -A, energia potencjalna jest największa, a energia kinetyczna – zerowa. 

Gdy mamy do czynienia z wahadłem matematycznym, to bez trudu za pomocą linijki lub taśmy mierniczej możemy zmierzyć jego długość, amplitudę drgań, a za pomocą stopera wyznaczyć okres. Jeżeli w czasie wykonywania doświadczenia nagramy ruch drgającego układu, to również nie sprawi nam trudności wyznaczenie dokładnych wysokości kulki wahadła nad położeniem równowagi.

Zastanówmy się, jak wyznaczyć największą szybkość osiąganą przez to wahadło. Do rozwiązania tego problemu skorzystamy z zasady zachowania energii mechanicznej. Zapiszmy, jakie energie posiada mała kulka zawieszona na nieważkiej nitce w poszczególnych etapach ruchu.

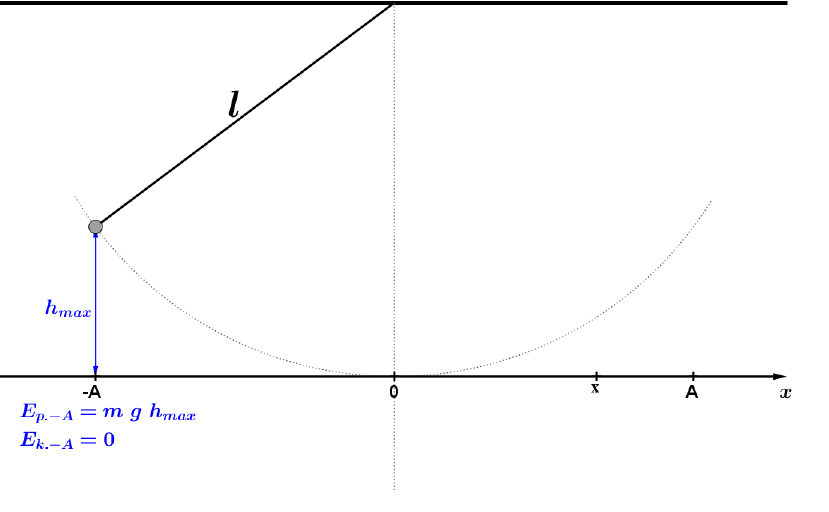
Ryc. 5. Pierwszy etap ruchu wahadła matematycznego

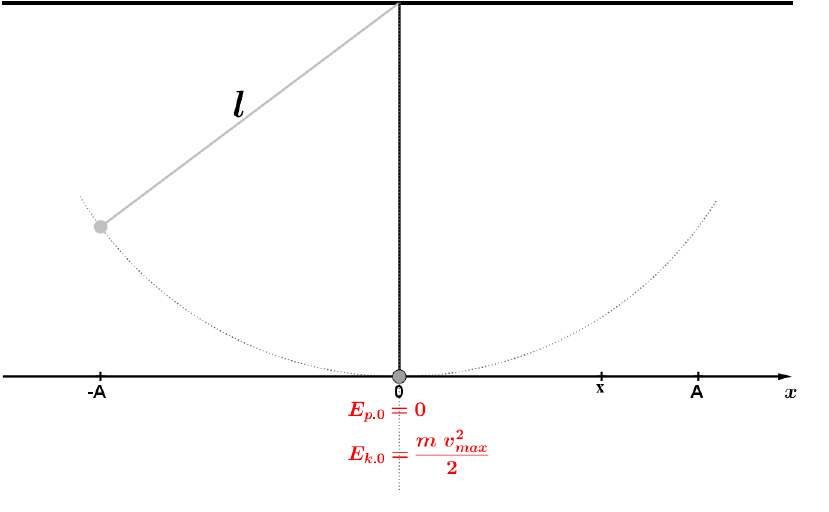
Ryc. 6. Drugi etap ruchu wahadła matematycznego

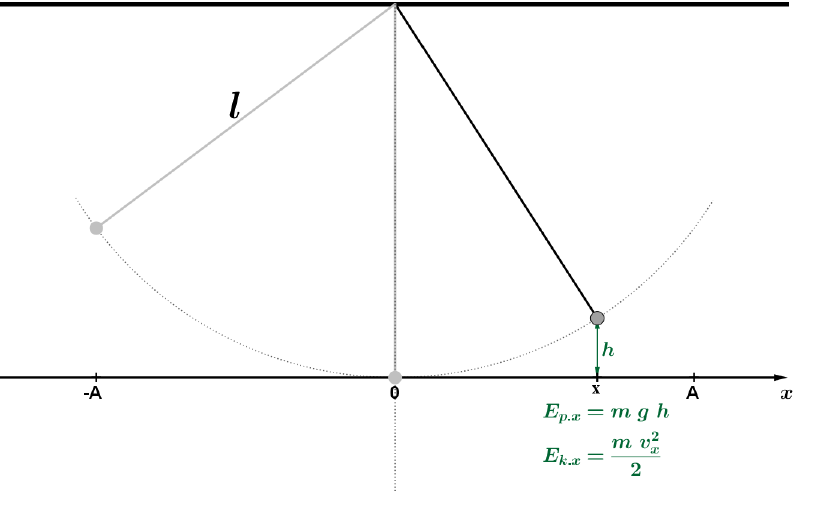
Ryc. 7. Trzeci etap etap ruchu wahadła matematycznego

Ryc. 8. Czwarty etap ruchu wahadła matematycznego

Zgodnie z zasadą zachowania energii spełnione jest równanie:

E{_{p.-A}}+E{_{k.-A}}=E{_{p.0}}+E{_{k.0}}=E{_{p.x}}+E{_{k.x}}=E{_{p.A}}+E{_{k.A}}

Oznacza to, że maksymalną szybkość osiąganą przez wahadło w najniższym położeniu możemy obliczyć za pomocą wzoru:

E{_{p.0}}+E{_{k.0}}=E{_{p.-A}}+E{_{k.-A}}

0+\frac{mv{_{max}}^2}{2}=mgh{_{max}}+0

v{_{max}}=\sqrt{2gh{_{max}}}

Natomiast szybkość w dowolnym położeniu pomiędzy położeniem równowagi a amplitudą spełnia równanie:

E{_{p.x}}+E{_{k.x}}=E{_{p.A}}+E{_{k.A}}

mgh + \frac{mv{_{x}}^2}{2}=mgh{_{max}}+0

\frac{mv{_{x}}^2}{2}=mgh{_{max}}-mgh

{v{_{x}}^2}=2g({h_{max}}-h)

v{_{x}}=\sqrt{2g(h{_{max}-h)}}

Energia ciała na sprężynie

Ciekawym przykładem zastosowania zasady zachowania energii jest rozważenie drgań ciała zaczepionego na sprężynie. Wówczas, oprócz energii potencjalnej ciężkości oraz energii kinetycznej, musimy rozważać energię potencjalną sprężystości.

Zobaczmy, jak przebiegają przemiany energii w takim przypadku.

Zawieszamy ciężarek na sprężynie

Nierozciągnięta sprężyna ma zerowe wydłużenie, a gdy powiesimy na niej ciężarek, jej wydłużenie wzrośnie, czyli wzrośnie również energia potencjalna sprężystości. Aby wprawić układ w drgania, musimy wydłużyć jeszcze dodatkowo sprężynę, działając na nią siłą naszych rąk. Wówczas rozciągnięcie sprężyny będzie maksymalne. Oznacza to, że gdy ciężarek znajduje się w najniższym możliwym położeniu, posiada najmniejszą możliwą energię potencjalną ciężkości. Ponieważ jednak jego wychylenie jest największe, to energia potencjalna sprężystości przyjmuje maksymalną wartość. Szybkość ciężarka w tym położeniu jest zerowa, czyli energia kinetyczna również jest zerowa.

Puszczamy ciężarek

Ciężarek znajdujący się w najniższym możliwym położeniu w wyniku działania siły sprężystości zacznie przemieszczać się w stronę położenia równowagi. Zatem ciężarek podnosi się coraz wyżej, sprężyna zmniejsza swoje wydłużenie, a szybkość ciężarka wzrasta. Oznacza to, że energia potencjalna ciężkości rośnie, energia potencjalna sprężystości maleje, a energia kinetyczna rośnie.

Ciężarek mija położenie równowagi

Gdy ciężarek minie położenie równowagi, sprężyna nadal kurczy się, czyli energia sprężystości wciąż maleje. W czasie tego ruchu zmniejsza się szybkość ciężarka, to znaczy, że energia kinetyczna maleje aż osiągnie zerową wartość. Ciężarek porusza się w stronę maksymalnego położenia, w związku z czym jego energia potencjalna ciężkości rośnie, a energia potencjalna sprężystości maleje.

Ciężarek wraca do położenia równowagi

Po tym, jak ciężarek znalazł się w swoim najwyższym położeniu, zaczyna on opadać. Wówczas aż do osiągnięcia położenia równowagi energia kinetyczna rośnie, by w nim osiągnąć maksymalną wartość. Energia potencjalna ciężkości maleje, ale w wyniku wydłużania się sprężyny energia potencjalna sprężystości rośnie aż osiągnie maksymalną wartość.

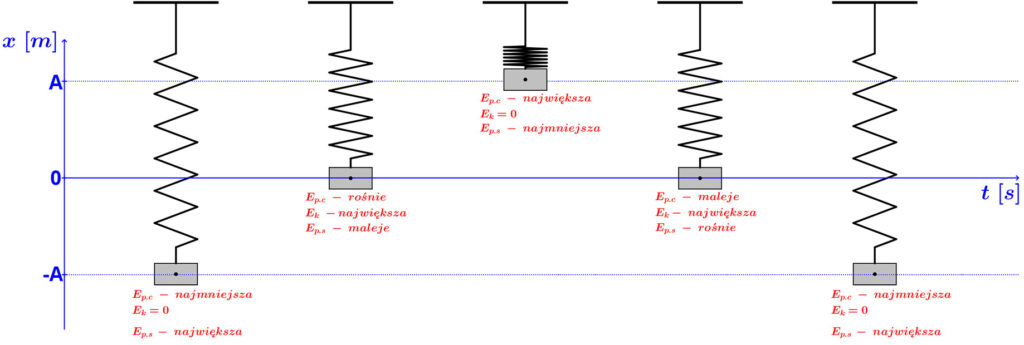
Ryc. 9. Przemiany energii w ruchu ciała zawieszonego na sprężynie

Podsumowanie

1. Praca mechaniczna jest wykonywana, gdy na ciało działa siła, w wyniku czego ciało to ulega przemieszczeniu lub odkształceniu.
2. Energia jest to wielkość fizyczna, która charakteryzuje stan układu.
3. Wyróżniamy następujące rodzaje energii mechanicznej:

• energia potencjalna ciężkości – związana z położeniem ciała względem pewnego poziomu zerowego,
• energia potencjalna sprężystości – związana z odkształceniem ciała, 
• energia kinetyczna – związana z ruchem ciała. 

4. Zasada zachowania energii: w izolowanym układzie suma wszystkich rodzajów energii układu jest stała w czasie.

Materiały źródłowe